Sắp xếp trộn – Merge Sort

Giới thiệu

Thuật toán sắp xếp Merge Sort là một trong những thuật toán có độ phức tạp ở mức trung bình và cùng sử dụng phương pháp chia để trị giống thuật toán sắp xếp nhanh Quicksort rồi gọi đệ quy chính nó trên các phân vùng đã chia. Thuật toán này không chỉ áp dụng trong sắp xếp mà còn ở nhiều bài toán khác. Sự khác biệt chính là Quicksort là thuật toán sắp xếp nội (internal), tại chỗ (in-place) trong khi đó Merge Sort lại là thuật toán sắp xếp ngoại (external), không tại chỗ (not-in-place).

Cài đặt

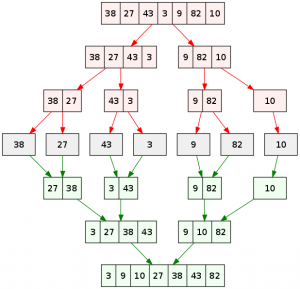
Thuật toán này chia mảng cần sắp xếp thành 2 nửa. Với phương thức mergeSort(), tiếp tục lặp lại việc này ở các nửa mảng đã chia cho đến khi chỉ còn 1 phần tử. Sau cùng gộp lại thành mảng đã sắp xếp. Phương thức merge() là tiến trình quan trọng nhất, được sử dụng để gộp hai nửa mảng thành 1 mảng duy nhất đã được sắp xếp.

Khởi đầu với phương thức mergeSort():

public static void mergeSort(int[] array, int low, int high) {

    if (high <= low) return;


    int mid = low + (high - low) / 2;

    mergeSort(array, low, mid);

    mergeSort(array, mid+1, high);

    merge(array, low, mid, high);

}

Phần này khá đơn giản, chúng ta có 1 mảng cần được sắp xếp, các con trỏ ở vị trí đầu và cuối. Nếu con trỏ ở vị trí cuối nhỏ hơn hoặc bằng vị trí con trỏ ở đầu thì trả về.

Mặt khác, chúng ta sẽ phân vùng mảng thành 2 nửa, gọi phương thức mergeSort() từ đầu đến giữa và từ giữa đến cuối.

Cuối cùng, gọi phương thức merge() để hợp nhất các kết quả thành một mảng đã được sắp xếp.

public static void merge(int[] array, int low, int mid, int high) {

    // Creating temporary subarrays

    int leftArray[] = new int[mid - low + 1];

    int rightArray[] = new int[high - mid];


    // Copying our subarrays into temporaries

    for (int i = 0; i < leftArray.length; i++)

        leftArray[i] = array[low + i];

    for (int i = 0; i < rightArray.length; i++)

        rightArray[i] = array[mid + i + 1];


    // Iterators containing current index of temp subarrays

    int leftIndex = 0;

    int rightIndex = 0;


    // Copying from leftArray and rightArray back into array

    for (int i = low; i < high + 1; i++) {

        // If there are still uncopied elements in R and L, copy minimum of the two

        if (leftIndex < leftArray.length && rightIndex < rightArray.length) {

            if (leftArray[leftIndex] < rightArray[rightIndex]) {

               array[i] = leftArray[leftIndex];

               leftIndex++;

            } else {

                array[i] = rightArray[rightIndex];

                rightIndex++;

            }

        } else if (leftIndex < leftArray.length) {

            // If all elements have been copied from rightArray, copy rest of leftArray

            array[i] = leftArray[leftIndex];

            leftIndex++;

        } else if (rightIndex < rightArray.length) {

            // If all elements have been copied from leftArray, copy rest of rightArray

            array[i] = rightArray[rightIndex];

            rightIndex++;

        }

    }

}

Chạy đoạn mã dưới đây:

int[] array = new int[]{5, 6, 7, 2, 4, 1, 7};

mergeSort(array);

System.out.println(Arrays.toString(array));

Và kết quả là một mảng được sắp xếp hoàn chỉnh:

[1, 2, 4, 5, 6, 7, 7]

Đánh giá thuật toán sắp xếp trộn

Độ phức tạp thuật toán:

• Trường hợp tốt: O(n*log(n))
• Trung bình: O(n*log(n))
• Trường hợp xấu: O(n*log(n))

Không gian bộ nhớ sử dụng: O(n)

Ổn định (Stable): Có

Tại chỗ (In-place): Không

Cách sử dụng:

• Merge Sort rất phù hợp để sắp xếp danh sách liên kết (Linked lists) trong thời gian O(n*log(n))
• Đếm ngược trong một mảng
• Sắp xếp ngoại