NỘI DUNG BÀI VIẾT
Giới thiệu
Dữ liệu trong một bảng biểu là một ví dụ đặc trưng về mảng hai chiều. Ví dụ, dữ liệu trong bảng sau đây:
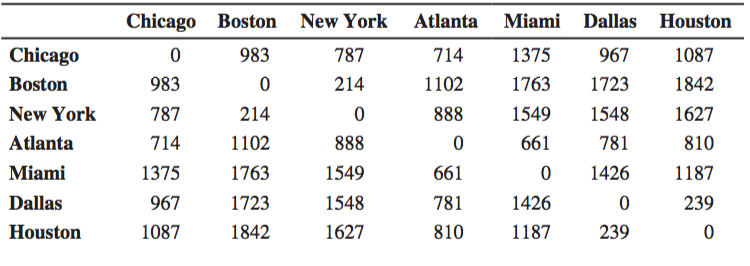
Có thể được diễn giải vào một mảng hai chiều như sau:
double[][] distances = {
{0, 983, 787, 714, 1375, 967, 1087},
{983, 0, 214, 1102, 1763, 1723, 1842},
{787, 214, 0, 888, 1549, 1548, 1627},
{714, 1102, 888, 0, 661, 781, 810},
{1375, 1763, 1549, 661, 0, 1426, 1187},
{967, 1723, 1548, 781, 1426, 0, 239},
{1087, 1842, 1627, 810, 1187, 239, 0},
};
Cơ bản về mảng hai chiều
Để tạo ra mảng hai chiều cần có thông tin về số hàng và số cột của mảng.
Vị trí của một phần tử trong mảng hai chiều được xác định bởi thông số hàng và cột. Thông qua vị trí, ta có thể lấy được giá trị của phần tử đó.
Tạo ra biến mảng hai chiều và tạo ra mảng hai chiều
Để khai báo một biến có kiểu là mảng hai chiều, ta có thể làm như sau (cách thứ hai không được khuyến khích nhưng vẫn được liệt kê ở đây):
elementType[][] arrayRefVar;
hoặc
elementType arrayRefVar[][];
Ví dụ, tạo một biến tên matrix có kiểu là một mảng hai chiều của các số nguyên:
int[][] matrix
Để gán một mảng hai chiều thật sự vào biến matrix, ta làm như sau:
matrix = new int[5][5]
Như ta quan sát thấy, ta cần có thông tin về số dòng và số cột của mảng để có thể tạo ra mảng. Java sẽ bố trí sẵn một mảng như hình (2a). Lưu ý quan sát số dòng và số cột được đếm bắt đầu từ 0.

Để truy xuất và gán giá trị cho một phần tử ở hàng 2 cột 1 trong mảng, như được mô tả trong hình (2b), ta làm như sau:
matrix[2][1] = 7;
Lưu ý: Lỗi thường gặp là nhầm lẫn giữa hàng và cột, cũng như sử dụng biểu thức
matrix[2, 1]thay vìmatrix[2][1].
Bạn cũng có thể khởi tạo nhanh mảng hai chiều như được biểu thị ở hình (2c). Mã ở hình (3a) và (3b) dưới đây là tương đương nhau:

Lấy chiều dài các chiều của mảng hai chiều
Một mảng hai chiều thực chất là một mảng mà mỗi phần tử là một mảng một chiều. Chiều dài của một biến mảng hai chiều x là số phần tử của mảng, được lấy bởi biểu thức x.length. x[0], x[1], …, x[x.length - 1] là các mảng mà chiều dài của chúng được truy cập bởi x[0].length, x[1].length, …, x[x.length - 1].length.
Điều đó được thể hiện bởi hình 4 dưới đây:

Ragged
Như đã nói ở trên, mảng hai chiều thực chất là một mảng của các mảng một chiều. Như vậy ta có thể trì hoãn việc tạo ra các mảng con, chỉ cần tạo ra mảng cha trước, như sau:
int[][] triangleArray = new int[5][]
Kéo theo đó, các mảng con có thể là các mảng mà có độ dài khác nhau, như sau:
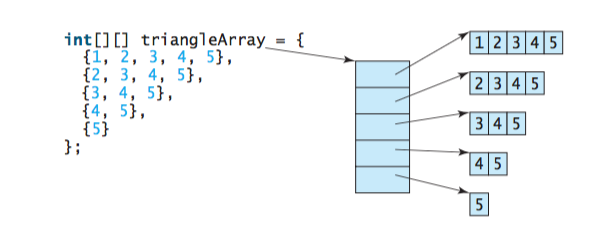
int[][] triangleArray = new int[5][]; triangleArray[0] = new int[5]; triangleArray[1] = new int[4]; triangleArray[2] = new int[3]; triangleArray[3] = new int[2]; triangleArray[4] = new int[1];
Mảng hai chiều mà chúng ta vừa được tạo ra có cấu trúc tương tự như mảng được biểu diễn trong hình dưới đây, do cấu trúc không cố định của nó, mảng này được gọi là Ragged Array(mảng “tơi tả”):
Xử lý mảng hai chiều
Những vòng lặp lồng nhau thường được sử dụng để xử lý trên một mảng hai chiều.
Đặt vấn đề chúng ta đã có một mảng được khai báo và tạo ra bởi dòng mã:
int[][] matrix = new int[10][10];
Dưới đây mã mẫu cho một số xử lý thường gặp trên mảng đó.
Nhập liệu các giá trị vào mảng
Chạy vòng lặp để đưa giá trị nhập liệu của người dùng vào mảng:
java.util.Scanner input = new Scanner(System.in);
System.out.println("Enter " + matrix.length + " rows and " +
matrix[0].length + " columns: ");
for (int row = 0; row < matrix.length; row++) {
for (int column = 0; column < matrix[row].length; column++) {
matrix[row][column] = input.nextInt();
}
}
Nhập các giá trị ngẫu nhiên vào mảng
Thay vì sử dụng giá trị nhập liệu từ người dùng, tạo ra giá trị ngẫu nhiên để gán vào các phần tử của mảng:
for (int row = 0; row < matrix.length; row++) {
for (int column = 0; column < matrix[row].length; column++) {
matrix[row][column] = (int) (Math.random() * 100);
}
}
In mảng
Sử dụng vòng lặp để in lần lượt từng phần tử một của mảng như trong khối lệnh dưới đây:
for (int row = 0; row < matrix.length; row++) {
for (int column = 0; column < matrix[row].length; column++) {
System.out.print(matrix[row][column] + " ");
}
System.out.println();
}
Tính tổng tất cả các phần tử trong mảng
Sử dụng một biến total để lưu trữ giá trị tổng, được khởi tạo với giá trị 0. Sử dụng vòng lặp để cộng lần lượt từng phần tử một của mảng vào biến này:
int total = 0;
for (int row = 0; row < matrix.length; row++) {
for (int column = 0; column < matrix[row].length; column++) {
total += matrix[row][column];
}
}
Tính tổng từng cột
Với mỗi cột, sử dụng một biến total để lưu trữ giá trị tổng, được khởi tạo với giá trị 0. Sử dụng vòng lặp để cộng lần lượt từng phần tử một của cột vào biến này:
for (int column = 0; column < matrix[0].length; column++) {
int total = 0;
for (int row = 0; row < matrix.length; row++)
total += matrix[row][column];
System.out.println("Sum for column " + column + " is "
+ total);
}
Tìm ra dòng có tổng các phần tử là lớn nhất
Sử dụng các biến maxRow và indexOfMaxRow để theo dấu tổng lớn nhất và định vị của dòng có tổng đó. Với mỗi dòng, tính tổng các phần tử của nó và cập nhật maxRow và indexOfMaxRow nếu dòng mới tính xong có tổng lớn hơn giá trị cũ:
int maxRow = 0;
int indexOfMaxRow = 0;
// Get sum of the first row in maxRow
for (int column = 0; column < matrix[0].length; column++) {
maxRow += matrix[0][column];
}
for (int row = 1; row < matrix.length; row++) {
int totalOfThisRow = 0;
for (int column = 0; column < matrix[row].length; column++)
totalOfThisRow += matrix[row][column];
if (totalOfThisRow > maxRow) {
maxRow = totalOfThisRow;
indexOfMaxRow = row;
}
}
System.out.println("Row " + indexOfMaxRow + " has the maximum sum of " + maxRow);
Xáo trộn mảng
Với mỗi phần tử matrix[i][j], tạo ra ngẫu nhiên hai định vị i1 và j1 trong khoảng cho phép và tráo đổi giá trị của hai phần tử matrix[i][j] và matrix[i1][j1] với nhau:
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
int i1 = (int) (Math.random() * matrix.length);
int j1 = (int) (Math.random() * matrix[i].length);
// Swap matrix[i][j] with matrix[i1][j1]
int temp = matrix[i][j];
matrix[i][j] = matrix[i1][j1];
matrix[i1][j1] = temp;
}
}
Mảng nhiều chiều
Mảng hai chiều là mảng của các mảng một chiều, và mảng ba chiều là mảng của các mảng hai chiều.
Đôi khi, ta gặp những dữ liệu cần được biểu diễn theo dạng mảng-n-chiều. Với Java, sử dụng cấu trúc mảng của các mảng, với bất cứ số nguyên dương n nào, ta có thê tạo ra mảng với n chiều.
Đặt vấn đề chúng ta cần lưu trữ điểm cho mỗi câu hỏi của của mỗi bài kiểm tra của các sinh viên. Dữ liệu đó là một mảng 3 chiều mà có thể được khai báo bằng câu lệnh sau đây:
double[][][] scores = new double[6][5][2];
Ta có thể tạo nhanh giá trị cho mảng scores bằng câu lệnh như dưới đây:
double[][][] scores = {
{{7.5, 20.5}, {9.0, 22.5}, {15, 33.5}, {13, 21.5}, {15, 2.5}},
{{4.5, 21.5}, {9.0, 22.5}, {15, 34.5}, {12, 20.5}, {14, 9.5}},
{{6.5, 30.5}, {9.4, 10.5}, {11, 33.5}, {11, 23.5}, {10, 2.5}},
{{6.5, 23.5}, {9.4, 32.5}, {13, 34.5}, {11, 20.5}, {16, 7.5}},
{{8.5, 26.5}, {9.4, 52.5}, {13, 36.5}, {13, 24.5}, {16, 2.5}},
{{9.5, 20.5}, {9.4, 42.5}, {13, 31.5}, {12, 20.5}, {16, 6.5}}};
%}
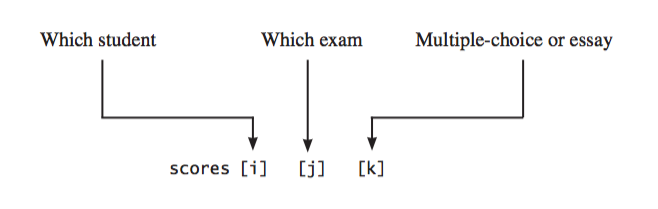
Ta có thể truy cập tới một giá trị điểm bất kỳ bằng cú pháp scores[0][1][2]. Nó chỉ tới điểm của câu hỏi số 3 của bài kiểm tra thứ 2 của sinh viên đầu tiên. Lược đồ sau làm rõ điều đó:
Tổng kết
Bài đọc này có những điểm đáng lưu ý sau:
- Mảng hai chiều có thể được sử dụng để lưu trữ các “bảng”.
- Một biến mảng hai chiều có thể được tạo ra bằng cú pháp
elementType[][] arrayVar - Một mảng hai chiều có thể được tạo ra bằng cú pháp
new elementType[ROW_SIZE][COLUMN_SIZE] - Mỗi phần tử trong mảng hai chiều được xác định bởi cú pháp
arrayVar[rowIndex][columnIndex] - Mảng hai chiều có thể được khai báo nhanh với cú pháp
elementType[][] arrayVar = {{row values}, . . . , {row values}} - Ta có thể sử dụng mảng của các mảng để cấu trúc nên mảng nhiều chiều.



